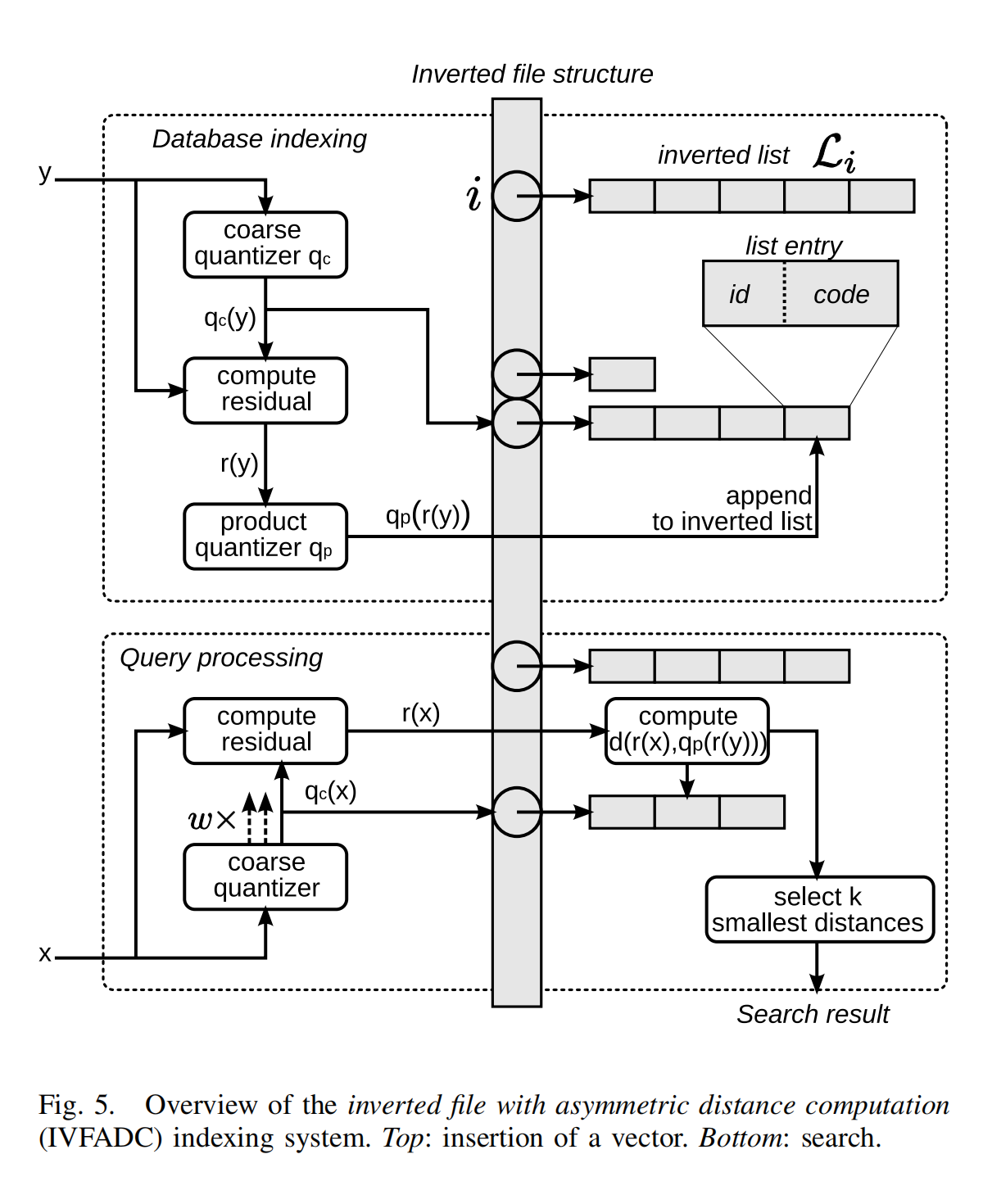
Product Quantization for Nearest Neighbor Search

https://ieeexplore.ieee.org/document/5432202

Product Quantization 是一种用于高维向量压缩和近似相似度搜索的技术。它的思想是将高维向量分割成多个较低维的子向量，并对每个子向量进行独立的量化。这种分割和量化的过程可以减少 Memory footprint 和计算成本，并且在一定程度上保持原始向量的相似性。

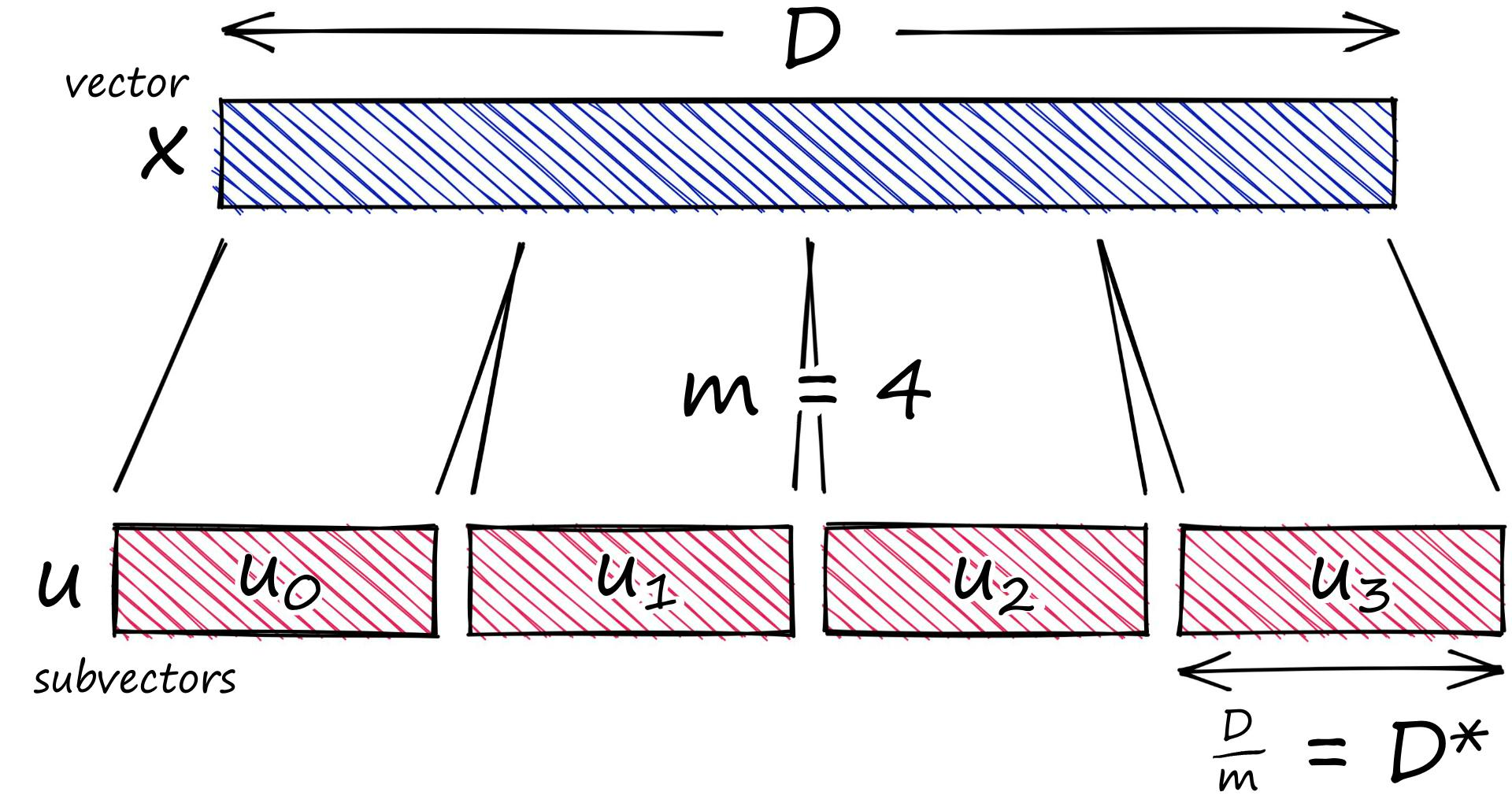
pq subvector

PQ 的两个参数:

  • m: 子向量的个数，需要保证 D % m = 0
  • k*: 对每个 D* 维的子向量进行聚类后 centroid 的个数（2 的幂次方）

The input vector x is split into m distinct subvectors uj , 1 ≤ j ≤ m of dimension D* = D/m, where D is a multiple of m. The subvectors are quantized separately using m distinct quantizers.

pq equations

PQ 的本质是将原始高维空间分解为多个低维子空间，并对这些子空间进行独立的量化。每个子空间的量化结果可以看作是一个码本（codebook），由一组离散的代表性向量构成。PQ 可以看作是对这些子空间的笛卡尔积进行编码。

PQ 计算举例的两种策略:

  • Symmetric distance computation (SDC): both the vectors x and y are represented by their respective centroids q(x) and q(y).
  • Asymmetric distance computation (ADC): the database vector y is represented by q(y), but the query x is not encoded.

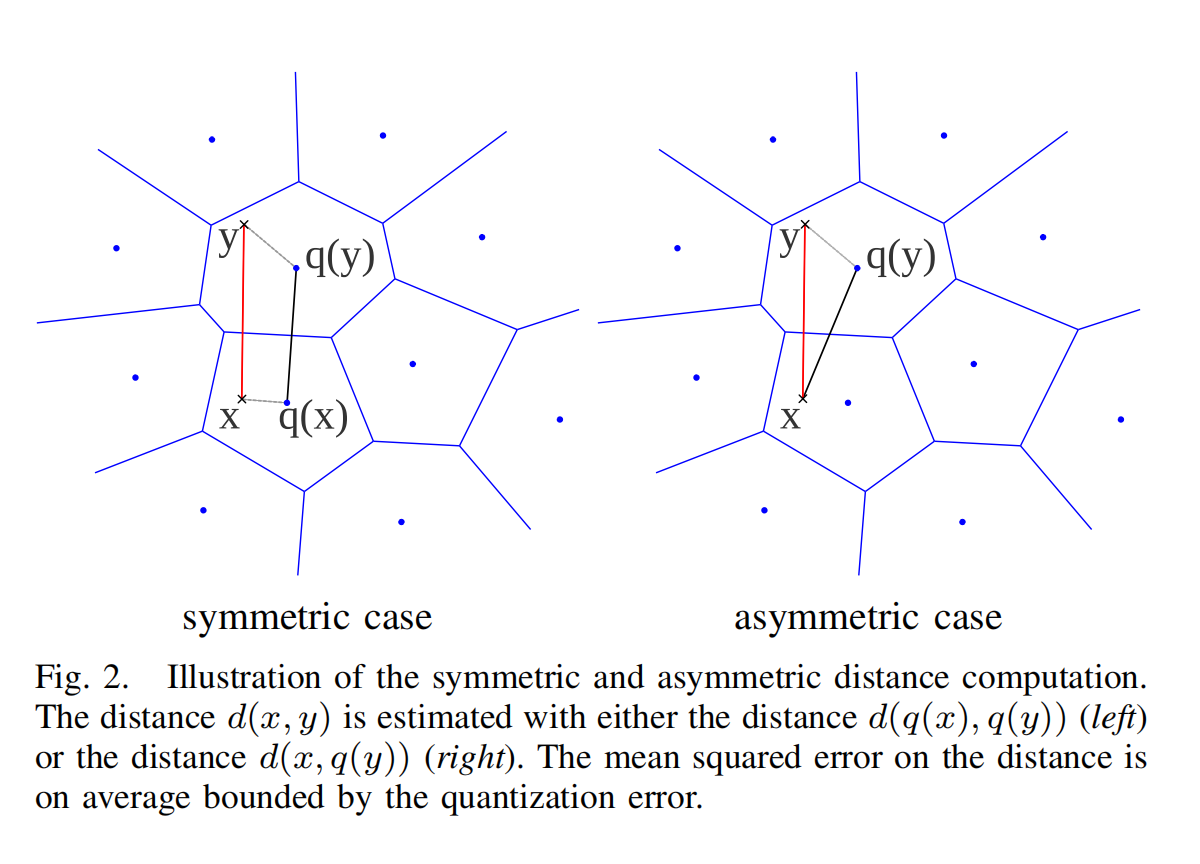
pq distance computation

SDC 需要对查询向量进行 quantization 之后去查询，距离计算转换为查表，ADC 不需要量化但需要计算距离。

The only advantage of SDC over ADC is to limit the memory usage associated with the queries, as the query vector is defined by a code. This is most cases not relevant and one should then use the asymmetric version, which obtains a lower distance distortion for a similar complexity.

PQ 是一种压缩算法，如果需要更快的检索速度，需要搭配一些其它算法来实现，如 IVFPQ。

IVFADC

References: