The Adaptive Radix Tree: ARTful Indexing for Main-Memory Databases
ICDE 2013
https://ieeexplore.ieee.org/document/6544812
Radix Tree,又叫做 Prefix Tree 或 Trie,通常被用作字符串的索引,具有以下特点:
- 树的高度(和复杂性)取决于 key 的长度,而非树中元素的个数
- 不需要对树进行 rebalance,同样的数据集以任何顺序插入都得到一样的树
- keys 按照字典顺序存储
- 从树根到叶子的路径隐式地代表了 key,因此可以根据路径重构出 key
在实现 Trie 的时候,需要选择 span 值(即用几个 bit 决定其下一级子节点个数,后用 s 代表)的大小,当 s 较小时,树高相对较高,但由于不存在空间浪费,其消耗的空间较小;当 s 较大时,树高相对较低,但存在一些节点的子节点很少,造成空间的浪费,进而使得索引的内存消耗很大。这是由于传统的 Trie 在选定了 span 之后,其 fanout 就固定了。
trie height = ⌈k/s⌉
fanout = 2^s
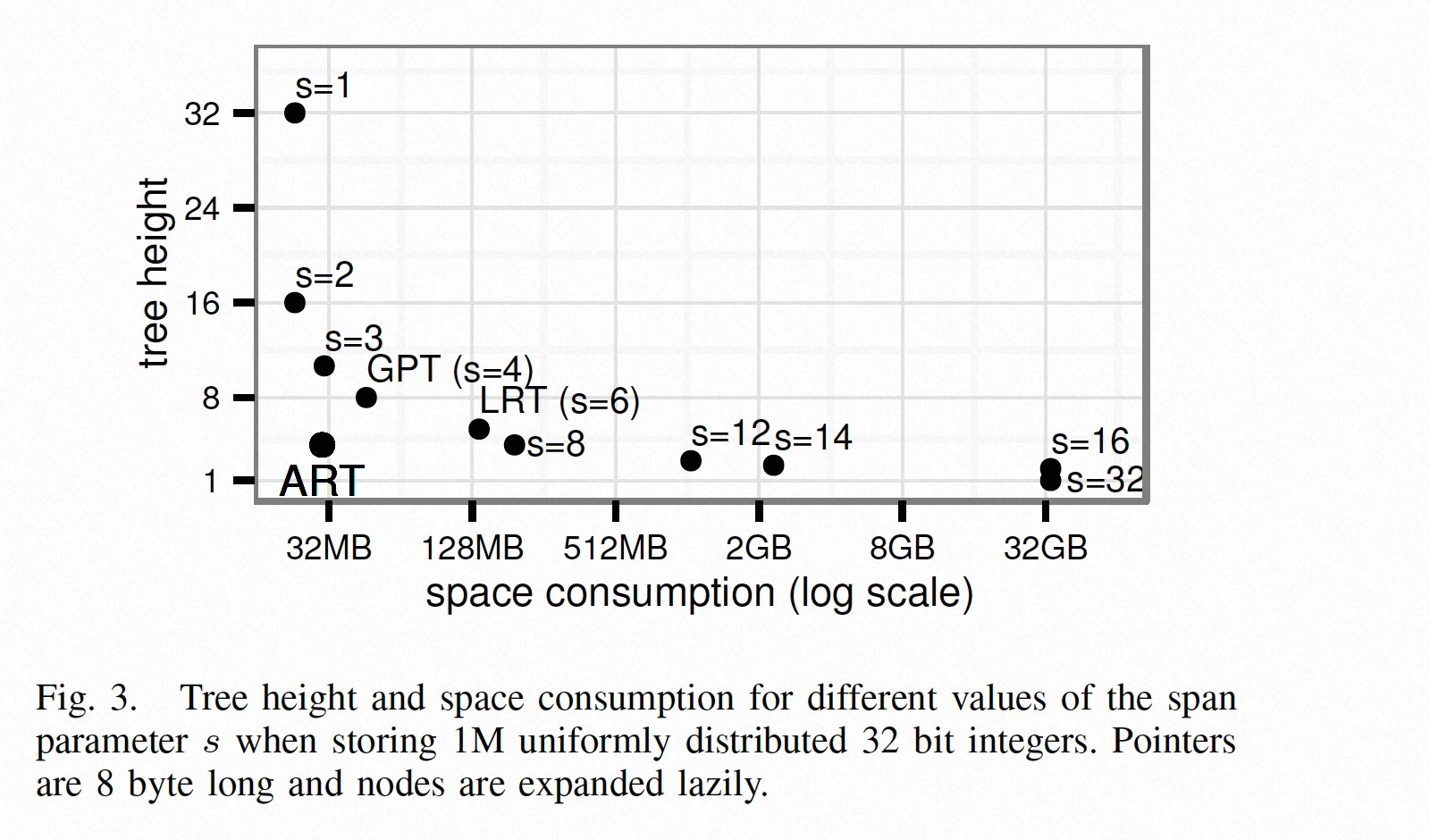
而 ART 则是在选择了较高 span 值(s = 8)的前提下,提供了四种不同 fanout 的节点,这样能够在保留 Trie 较低树高的前提下节省了空间使用,从上图中可以看出,ART 的树高与 s=8 的前缀树树高相同,但其内存消耗却只相当于 s=3 的前缀树。下图展示了 ART 的设计思想:
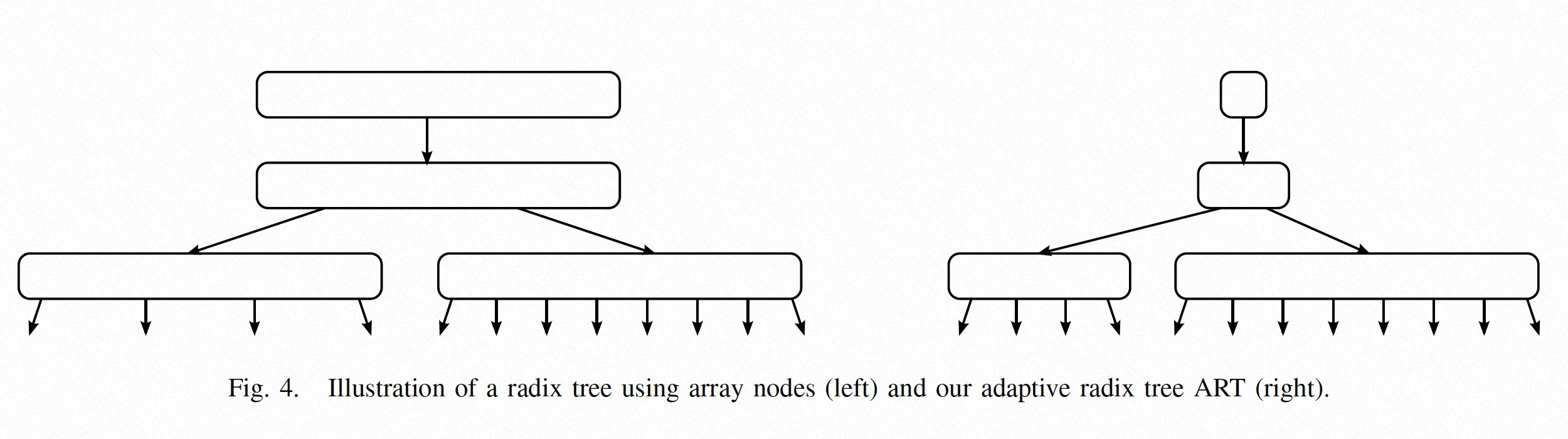
ART 使用了四种 Inner Node 结构和 Leaf Nodes,Inner Nodes 的结构如下图:
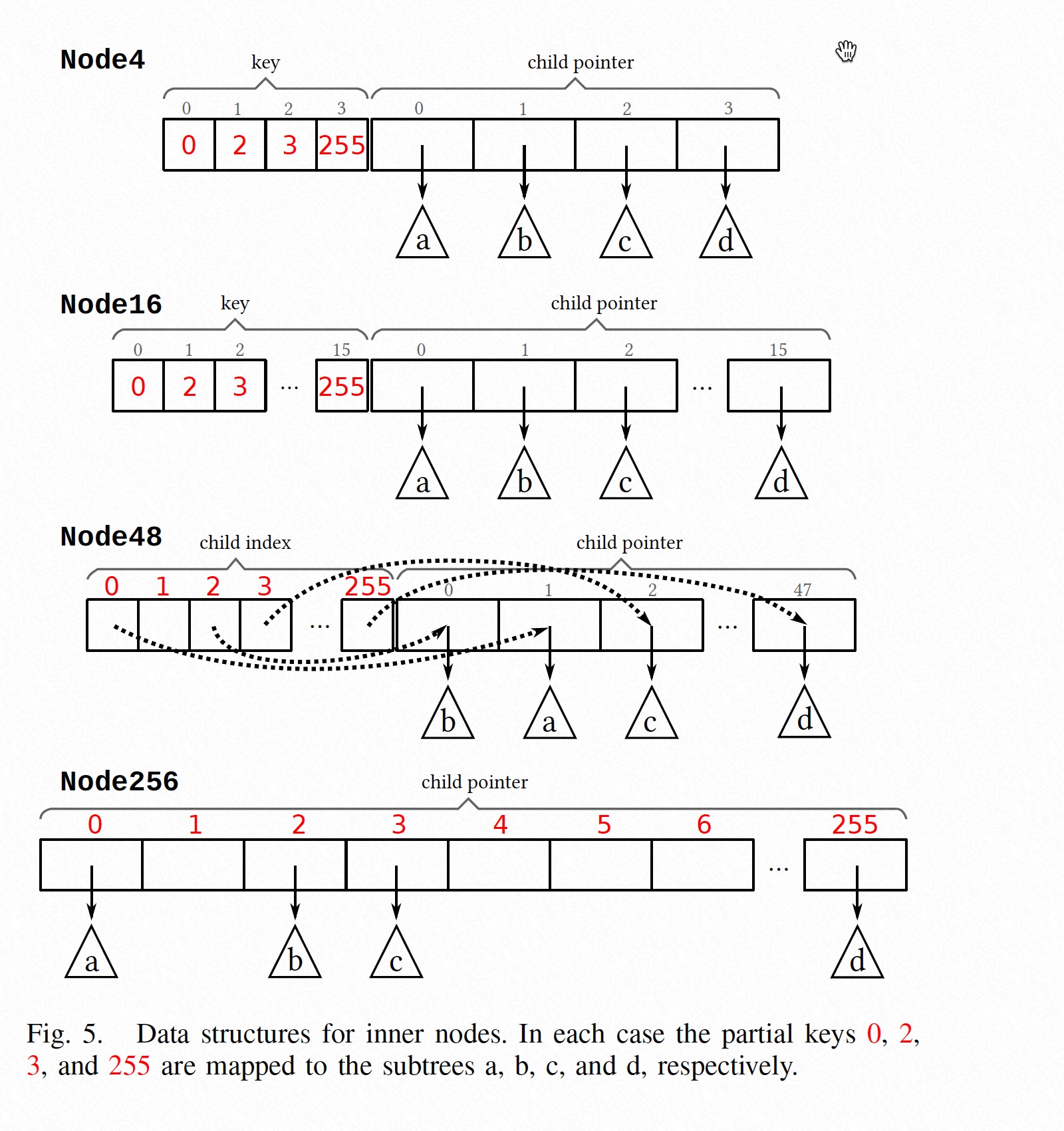
ART 还使用了 lazy expansion 和 path compression 来进一步缩小存储空间:
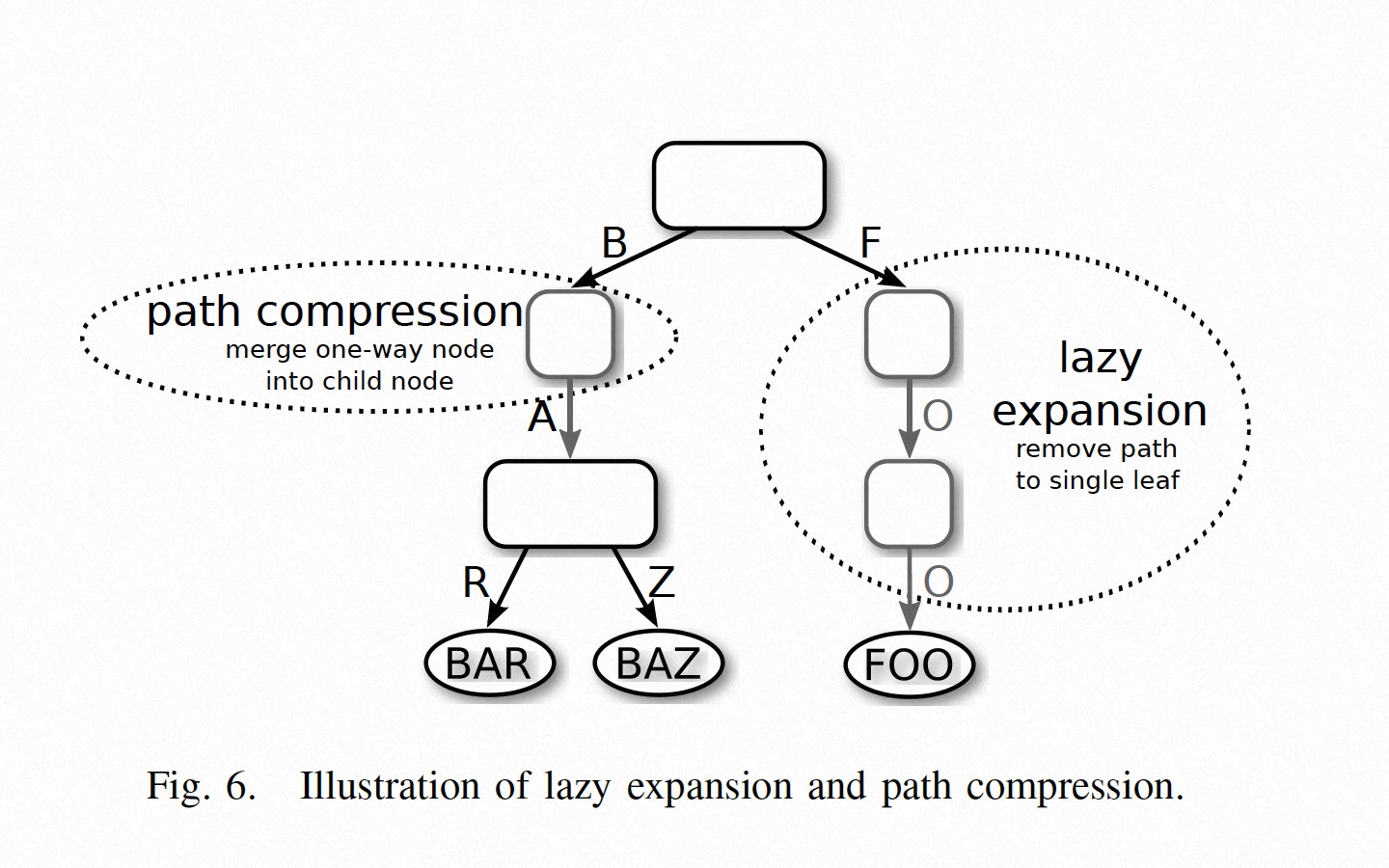
论文中虽然描述了算法的伪代码,但非常推荐结合 libart 代码一起看。
另外一个值得说明的一点,不同于直接比较 key 的数据结构(hash or comparison-based search trees),要想将 trie 用作通用的索引结构,还需要将 key 转化为 Binary-comparable key。
Keys stored in radix trees are ordered bitwise lexicographically. For some data types, e.g., ASCII encoded character strings, this yields the expected order. For most data types this is not the case.
However, it is possible to obtain the desired order by transforming the keys. We call the values resulting from such a transformation binary-comparable keys.
需要转化的类型有:
- Unsigned Integers
- Signed Integers
- IEEE 754 Floating Point Numbers
- Character Strings
- Null
如对于 Unicode 字符串,可以使用 The Unicode Collation Algorithm 定义的规则进行比较。